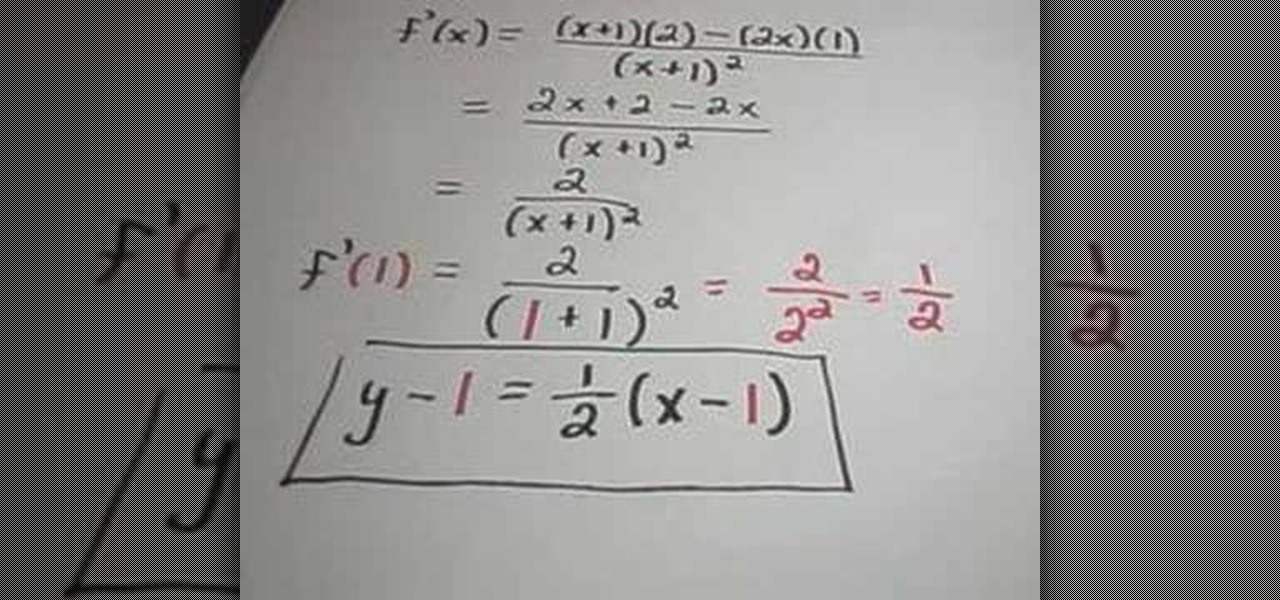The problem of finding the slope of the tangent line to a curve and the problem of finding the instantaneous velocity of an object both involve finding the same type of limit. Want to find the slope of the line tangent to the graph of this function at the X. So the slope of a tangent line is the same as the instantaneous velocity which is the same as a derivative. So we're going to do to the limit as a church approaches zero of our F F x plus H minus F.
So F. Of I can do negative three plus H but I like H minus three better -F. So we're going to do some work on this side. We have negative five times negative three plus six. 21 is going to go right there for f of negative three And we're gonna find f of H -3.
I mean negative five times H -3 plus six. Just should be the negative five, negative five. Plus 21 so that's going to go right there. So we have now the limit as a church approaches zero of negative five H. We have negative five nowhere to plug in the H approaching zero.
Using differential calculus, we can determine the limit, or the value that Δy/Δx approaches as Δy and Δx get closer to zero; it follows that this limit is the exact slope of the tangent. If y is dependent on x, then it is sufficient to take the limit where only Δx approaches zero. Therefore, the slope of the tangent is the limit of Δy/Δx as Δx approaches zero, or dy/dx. The concept of a slope is central to differential calculus.
For non-linear functions, the rate of change varies along the curve. The derivative of the function at a point is the slope of the line tangent to the curve at the point, and is thus equal to the rate of change of the function at that point. So, how does this help us with the tangent line? Well, imagine that we took that second point (a + h , f(a + h)) and brought it closer to our first point. The closer it gets to the first point, the more the secant line starts to resemble the tangent line!
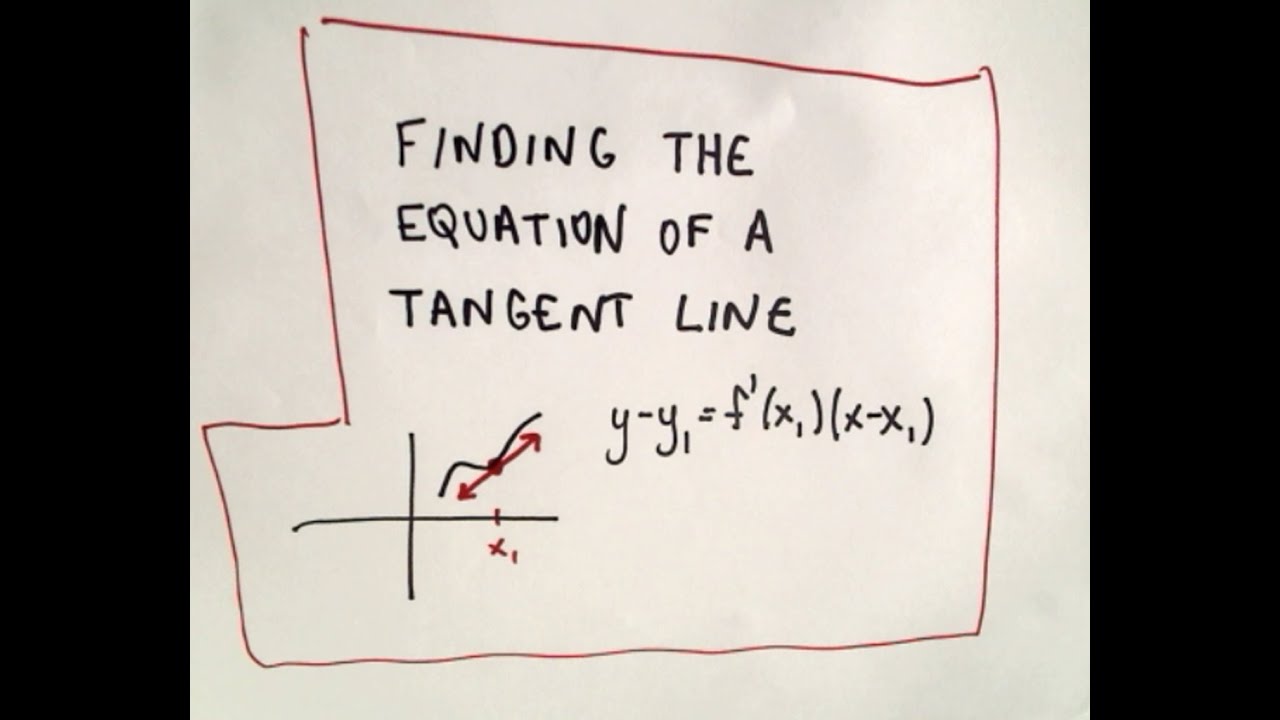
We bring it closer and closer and closer… which is the mathematical idea of a limit. As h approaches zero, this turns our secant line into our tangent line, and now we have a formula for the slope of our tangent line! It is the limit of the difference quotient as h approaches zero. Let's take a couple of moments to review what a tangent line is and what its equation is. A tangent line is a straight line that just barely touches a curve at one point.
The idea is that the tangent line and the curve are both going in the exact same direction at the point of contact. The slope, or the steepness, of the tangent line is determined by the function's instantaneous rate of change at that point. The slope of the line is found by creating a derivative function based on a secant line's approach to the tangent line. A secant line is a line that connects two points on a curve. Together we will walk through three examples and learn how to use the point-slope form to write the equation of tangent lines and normal lines. So in this sense, calling it a tangent line seems reasonable.
However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function. We should note that in the particular case of a circle, there's a simple way to find the derivative. Since the tangent to a circle at a point is perpendicular to the radius drawn to the point of contact, its slope is the negative reciprocal of the slope of the radius. The radius joining $$ to $$ has slope 24/7. Hence, the tangent line has slope $-7/24$.
In general, a radius to the point $\ds (x,\sqrt)$ has slope $\ds \sqrt/x$, so the slope of the tangent line is $\ds $, as before. It is NOT always true that a tangent line is perpendicular to a line from the origin—don't use this shortcut in any other circumstance. As the second value $7+\Delta x$ moves in towards 7, the chord joining $(7,f)$ to $(7+\Delta x,f(7+\Delta x))$ shifts slightly. You can drag the red dot labeled $f(x+\Delta x)$ to watch this happen; the fixed red line is the tangent line. As a generalization of this practical description, the mathematics of differential calculus defines the slope of a curve at a point as the slope of the tangent line at that point.
When the curve is given by a series of points in a diagram or in a list of the coordinates of points, the slope may be calculated not at a point but between any two given points. Since the tangent line touches the circle at just one point, we will never be able to calculate its slope directly, using two "known" points on the line. What we need is a way to capture what happens to the slopes of the secant lines as they get "closer and closer" to the tangent line.
The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′. Likewise, we can even extend this concept to writing equations of normal lines, which are also called perpendicular lines.
The only difference will be that we will simply use the negative reciprocal slope of the line tangent. Let's briefly look at the velocity problem. Many calculus books will treat this as its own problem. We however, like to think of this as a special case of the rate of change problem.
In the velocity problem we are given a position function of an object, \(f\left( t \right)\), that gives the position of an object at time \(t\). Then to compute the instantaneous velocity of the object we just need to recall that the velocity is nothing more than the rate at which the position is changing. Drag the red point to see how the tangent changes along the curve.
Drag the green point to see how the secant line approaches the tangent as the green dot approaches the red dot . Not also how each of the slopes of the tangent and secant lines change . Many common questions asked on the AP Calculus Exams involve finding the equation of a line tangent to a curve at a point. If we are adept at quickly taking derivatives of functions, then 90 percent of the work for these types of problems is done. Everything else comes down to quick algebra.
Normal lines aren't really that difficult to understand. All they are are lines that are perpendicular to tangent lines. As \(\Delta x\) is made smaller , \(7+\Delta x\) gets closer to 7 and the secant line joining \((7,f)\) to \((7+\Delta x,f(7+\Delta x))\) shifts slightly, as shown in Figure 4.1. This is actually quite difficult to see when \(\Delta x\) is small, because of the scale of the graph. The values of \(\Delta x\) used for the figure are \(1\text\) \(5\text\) \(10\) and \(15\text\) not really very small values. The tangent line is the one that is uppermost at the right hand endpoint.
Also, do not worry about how I got the exact or approximate slopes. We'll be computing the approximate slopes shortly and we'll be able to compute the exact slope in a few sections. Then take the limit of the slopes of the secant lines to find the derivative. Indeed, as we will soon see, the slope of the tangent line at $$ corresponds to the instantaneous velocity this object is traveling at some time $t_0$. Understanding the nature of slopes of tangent lines to functions can raise red flags when appropriate to alert us to not be so quick to believe what we see on our calculator screens. As with the tangent line problem all that we're going to be able to do at this point is to estimate the rate of change.
So, let's continue with the examples above and think of \(f\left( x \right)\) as something that is changing in time and \(x\) being the time measurement. Again, \(x\) doesn't have to represent time but it will make the explanation a little easier. While we can't compute the instantaneous rate of change at this point we can find the average rate of change. The slope of the tangent line to the graph of a function at a point is called the derivative of the function at that point.
The formal definition of derivative is given below. Secant line that connects two points, and instantaneous velocity corresponds to the slope of a line tangent to the curve. Suppose that the $x$-axis now represents time, and the $y$-axis represents the position/height of some object -- perhaps a rising red balloon. The slope of the tangent line is then a distance traveled divided by an elapsed time and can thus be interpreted as a velocity. The tangent line to a curve at a given point is the line which intersects the curve at the point and has the same instantaneous slope as the curve at the point. Finding the tangent line to a point on a curved graph is challenging and requires the use of calculus; specifically, we will use the derivative to find the slope of the curve.
Let's now look at the right graph of the above figure. What happens when we move point B towards point A? When the point B' is infinitesimally close to A, the secant line would turn into a line that touches the curve only once. Here the x coordinate of B' is (x0+h), with h an infinitesimally small value.
The corresponding value of the y-coordinate of the point B' is the value of this function at (x0+h), i.e., f(x0+h). So now we have a single, simple formula, $\ds $, that tells us the slope of the tangent line for any value of $x$. This slope, in turn, tells us how sensitive the value of $y$ is to changes in the value of $x$.
So far we have found the slopes of two chords that should be close to the slope of the tangent line, but what is the slope of the tangent line exactly? Next, let's find the equations of the lines that are normal to the curve at these two points. To write the equation of a line, we need to know its slope, and one point on the line. In the particular case of a circle, there's a simple way to find the derivative.
The radius joining \(\) to \(\) has slope 24/7. Hence, the tangent line has slope \(-7/24\text\) In general, a radius to the point \(\ds (x,\sqrt)\) has slope \(\ds \sqrt/x\text\) so the slope of the tangent line is \(\ds \text\) as before. ¶Before we embark on setting the groundwork for the derivative of a function, let's review some terminology and concepts. Remember that the slope of a line is defined as the quotient of the difference in y-values and the difference in x-values.
The derivative of a function has many applications to problems in calculus. It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values. A tangent line is simply a straight line, barely touching a curve at a single point. Understand the definition and visualize this mathematical function using examples of tangent equations on a graph.
Finding the slope of a tangent line and the equation of a tangent line of a function at a single point using limits. 2.4 RATES OF CHANGE & TANGENT LINES. Average Rate of Change The average rate of change of a quantity over a period of time is the slope on that interval. The below image shows three such secants $\overline$, $\overline$, and $\overline$. Note, the slopes of these secants do a better job of approximating the slope of the tangent line to the curve at $P$ shown in red as the second point $Q_i$ gets closer to $P$.
In the discussion above, we refer repeatedly to a tangent line to a function at some point. In geometry, one normally defines a tangent as a line that intersects a curve at only one point. Will this definition suffice for our purposes?
The slope of a line, and its relationship to the tangent line of a curve is a fundamental concept in calculus. It is important for a general understanding of function derivatives. OK, so we know how to find the slope of the tangent line really easily. All we have to do is find the derivative and plug x and/or y into the derivative to get the slope.
There is another thing we can do with the slope of the tangent line. Our final answer is the two equations with the green checkmarks next to them, and we've plotted those two lines, and the orignal function's curve, on the lower graph below. BUT, much more important is the process we used to find those equations, and we hope that makes sense.
In the graph above the tangent line is again drawn in red. The tangent touches the curve at (2.3, 5). Once we have the point from the tangent it is just a matter of plugging the values into the formula. The upshot is that this problem, finding the velocity of the ball, is exactly the same problem mathematically as finding the slope of a curve. Rather than ignoring the relationship between the two points, as in the first form, this formula relies upon it.
The symbol y2 is now f(x + h), and y1 is f. The major difference here, though, is that x2 has been replaced by the first x plus some change "h". The slope formula's premise still stands, however, as the new form does in fact calculate change in y over change in x. What we want is a line tangent to the function at (1, 1/2) -- one that has a slope equal to that of the function at (1, 1/2). In reality there probably won't be 15 cm3 more air in the balloon after an hour. The rate at which the volume is changing is generally not constant so we can't make any real determination as to what the volume will be in another hour.
In other words, as we take \(Q\) closer and closer to \(P\) the slope of the secant line connecting \(Q\) and \(P\) should be getting closer and closer to the slope of the tangent line. If you are viewing this on the web, the image below shows this process. So here is how we can "approach" that tangent line as a limit.